Effective Annual Rate Calculator: Compare True Interest Costs
Calculate the Effective Annual Rate (EAR) using the formula: EAR = (1 + r⁄n)n – 1, where r is the nominal interest rate (decimal form) and n is the number of compounding periods per year. For example, if the nominal interest rate is 10% (r = 0.10) and compounded quarterly (n = 4), the EAR is: EAR = (1 + 0.10⁄4)4 – 1 = 10.38%.
Effective Annual Rate Calculator
Effective Annual Rate Calculator
Note: The Effective Annual Rate (EAR) shows the true annual interest rate when compounding is considered. It helps compare financial products with different compounding periods on an equal basis.
Beyond the Numbers: Essential EAR Calculator Insights
Get accurate results in seconds:
- Enter your nominal interest rate (the advertised percentage)
- Select your compounding frequency (monthly is most common)
- Click “Calculate EAR” to reveal the true annual rate
Quick Tip: Try comparing different compounding frequencies with the same nominal rate to see how dramatically your actual costs change!
Did you know? Most people don’t realize that two identical-looking 5% loans can have completely different actual costs depending on how often interest compounds.
That attractive 5% mortgage rate? It’s actually costing you more:
- 5% compounded annually = 5.00% EAR
- 5% compounded monthly = 5.12% EAR
- 5% compounded daily = 5.13% EAR
On a $300,000 30-year mortgage, daily vs. annual compounding costs you an extra $8,500!
Pro Move: When negotiating loans, focus on getting lower compounding frequency rather than fighting over tiny nominal rate differences.
Warning Sign: Lenders advertising extremely low rates often hide higher compounding frequencies in the fine print.
Match the right compounding frequency to your financial goals:
For Borrowing (lower is better):
- Annual: Best for borrowers (lowest EAR)
- Semi-annual: Common for bonds and some loans
- Monthly: Standard for mortgages and credit cards
For Investing (higher is better):
- Quarterly: Typical for dividends and some CDs
- Daily: Maximizes returns on savings accounts
- Continuous: The theoretical maximum (rarely offered)
Smart Strategy: For savings, seek daily compounding. For loans, negotiate for annual compounding. The difference could fund your next vacation!
Stop using APR for these critical comparisons:
- Investment comparison: Two CDs with identical APRs but different compounding frequencies will have different actual returns
- Credit card analysis: Credit cards typically compound daily, making their true cost higher than the stated APR
- Long-term planning: The longer the time period, the more crucial EAR becomes (compounding effects multiply over time)
Financial Pro Tip: Lenders advertise APR because it looks lower. Calculate EAR yourself to reveal what you’re really paying.
Real-world hack: When comparing investment options with identical nominal rates, the one with more frequent compounding will always make you more money—sometimes thousands more over time.
Details
- by Rhett C
- Updated August 25, 2025
- Add to your website
Why send your precious traffic to a 🤬 competitor when customers can crunch numbers right on your turf?
Fill out this quick form (takes 37 seconds, we timed it) & your custom calculator zooms into your inbox faster than you can say “conversion rate 💥”.

🔥 Compare APYs, not rates, to see true savings growth
🔥 Calculate EAR to uncover hidden loan costs
🔥 Daily compounding outperforms monthly over time
🔥 Lenders push nominal rates; savings show APY for a reason
🔥 Small EAR differences compound into big money
Understanding the True Cost and Return: The Effective Annual Rate for US Financial Decisions
Ever notice how banks advertise one interest rate, but you seem to earn (or pay) something different? That disconnect has a name: the Effective Annual Rate.
The EAR cuts through the marketing fog to reveal what you're actually earning on investments or paying on loans once compounding enters the picture. It shows the genuine rate after all the mathematical dust settles over a one-year period.
You might encounter this same concept under different aliases: effective interest rate (EIR), annual equivalent rate (AER), or annual percentage yield (APY) when talking about savings. The financial world loves its alphabet soup, doesn't it?
Why does the EAR matter more than the nominal rate splashed across advertisements? Because that nominal rate—the one displayed in eye-catching font—tells only half the story. It completely ignores how interest compounds throughout the year.
Think about it: interest that compounds monthly or daily creates a snowball effect that the nominal rate doesn't capture.
The EAR adjusts that nominal rate to account for compounding's cumulative impact, revealing the total interest earned or paid by year's end. This isn't just financial trivia—it directly impacts your bottom line.
For borrowers, the EAR gives you the unvarnished truth about what that loan actually costs. Often, it reveals you're paying more than the flashy advertised rate suggests.
For investors, the EAR (or APY) provides a level playing field for comparing different opportunities, regardless of how often they compound interest. It's like having a universal translator for financial products.
Decoding the EAR Formula
Behind every financial calculation lies a formula, and the EAR is no exception. But don't worry—this one's surprisingly straightforward once you break it down:
EAR = (1 + i/n)^n – 1
Let's decode what each piece means:
'i' represents the nominal annual interest rate, expressed as a decimal. So that enticing 7% rate becomes 0.07 when you're actually crunching the numbers.
'n' is the number of times interest compounds within a year. This is where the magic—or sometimes the hidden cost—happens.
Common compounding periods include:
- Annually (n=1)
- Semi-annually (n=2)
- Quarterly (n=4)
- Monthly (n=12)
- Daily (n=365)
Want to see how this plays out in real life? Let's walk through a few examples.
Imagine a loan with a 10% nominal rate compounded just once a year. With n=1, your EAR calculation is (1 + 0.10/1)^1 – 1 = 10%. No surprise here—when compounding happens only annually, the effective rate matches the nominal rate exactly.
But what happens when that same 10% loan compounds monthly? Now n=12, and the EAR becomes (1 + 0.10/12)^12 – 1, which equals approximately 10.47%.
That seemingly small difference of 0.47% can translate to hundreds or even thousands of extra dollars over the life of a substantial loan.
Let's try one more: a savings account offering 8% compounded daily (n=365). Your EAR would be (1 + 0.08/365)^365 – 1, which comes to about 8.33%.
These examples highlight why the frequency of compounding matters as much as the rate itself. More frequent compounding amplifies your effective rate—which is wonderful when you're earning interest but potentially painful when you're paying it.
The Power of Compounding Frequency
The gap between nominal and effective rates doesn't appear by magic—it's created by the financial world's most powerful force: compound interest.
What makes compound interest special? Unlike simple interest, it calculates returns not just on your initial principal but also on any interest already earned. It's literally "interest on interest," and depending on which side of the transaction you're on, it can be your best friend or your silent enemy.
How often compounding occurs—the frequency—determines how many times within a year your earned interest starts working for you (or against you if you're borrowing). Each compounding event is like a mini-reset where that new interest joins your principal and starts earning its own return.
Here's something to remember: for any fixed nominal rate, the EAR will always be equal to or higher than that nominal rate. And as compounding frequency increases, so does that difference.
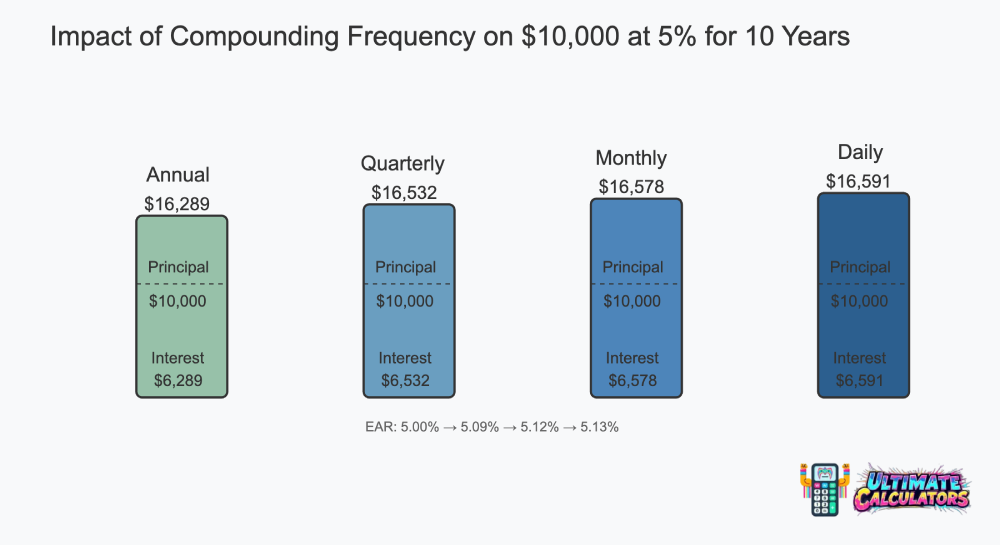
Want to see this in action? Check out this table showing how the same 5% nominal rate transforms depending on compounding frequency:
| Compounding Frequency | Number of Compounding Periods (n) | EAR Calculation | Effective Annual Rate (EAR) |
|---|---|---|---|
| Annually | 1 | (1 + 0.05/1)^1 - 1 | 5.00% |
| Semi-Annually | 2 | (1 + 0.05/2)^2 - 1 | 5.06% |
| Quarterly | 4 | (1 + 0.05/4)^4 - 1 | 5.09% |
| Monthly | 12 | (1 + 0.05/12)^12 - 1 | 5.12% |
| Daily | 365 | (1 + 0.05/365)^365 - 1 | ~5.13% |
Even at a modest 5% nominal rate, you can see how the effective rate inches upward with more frequent compounding. This difference becomes much more significant with higher interest rates—something to watch carefully with credit cards and other high-interest debt.
The table illustrates why the stated annual rate is just the starting point of the conversation. The compounding frequency is what determines your actual annual return or cost.
Navigating Related Financial Rates: EAR, Nominal Rate, APR, and APY
Ever feel like you need a financial dictionary just to understand your bank statements? Let's decode the alphabet soup of interest rates you'll encounter in your financial journey.
flowchart TB
START["Looking at Financial Products"] --> QUESTION["Borrowing or Investing?"]
QUESTION -->|"Borrowing"| BORROW["Evaluating Loan/Credit Options"]
QUESTION -->|"Investing"| INVEST["Evaluating Savings/Investment"]
BORROW --> LOOKB["Look Beyond Advertised Rate"]
LOOKB --> CALCEAR["Calculate EAR Using the Formula:<br/>(1 + i/n)^n - 1"]
CALCEAR --> COMPFEE["Consider Fees & Other Costs<br/>(May be in APR)"]
COMPFEE --> COMPAREB["Compare Total Cost<br/>Not Just Monthly Payment"]
COMPAREB --> WATCHCOMP["Watch for Compounding Frequency<br/>Higher Frequency = Higher Cost"]
INVEST --> LOOKI["Look for APY<br/>(equivalent to EAR)"]
LOOKI --> COMPAREI["Compare APYs Directly<br/>(Not Nominal Rates)"]
COMPAREI --> CHECKRISK["Check Risk Level &<br/>Liquidity Requirements"]
CHECKRISK --> WATCHFEE["Watch for Hidden Fees<br/>That Reduce Real Returns"]
WATCHCOMP --> DECISION["Make Informed Financial Decision"]
WATCHFEE --> DECISIONThe nominal annual interest rate is your starting point—the basic, advertised rate before any compounding works its magic. Think of it as the foundation upon which other rates are calculated.
In the US financial landscape, you'll frequently encounter the Annual Percentage Rate (APR) when shopping for loans. While it aims to give you a comprehensive view of borrowing costs, there's an important nuance—APR often includes fees and assumes interest is paid off at regular intervals, which might differ from the pure compounding effect that EAR captures.
Thanks to the Truth in Lending Act, lenders must disclose the APR to borrowers. This promotes transparency, but remember: APR and EAR aren't always directly equivalent because APR calculations frequently include additional costs beyond just interest.
What about when you're earning money instead of borrowing it? That's where Annual Percentage Yield (APY) comes into the picture. APY is essentially the twin of EAR specifically for savings accounts, certificates of deposit (CDs), and similar investment vehicles.
APY automatically accounts for compounding and reflects the actual percentage return you'll earn over a year. When financial institutions advertise deposit products, they typically highlight the APY because it presents a more attractive figure than the nominal rate, thanks to compounding's boost.
Understanding these distinctions becomes crucial when making financial decisions. When comparing loan offers, examining the EAR (or understanding what goes into the APR) gives you a clearer picture of the true cost of borrowing. A loan with a lower nominal rate but more frequent compounding might actually cost more than one with a slightly higher rate but less frequent compounding.
Conversely, when evaluating savings accounts or CDs, the advertised APY should be your focus since it already factors in compounding's effects.
Here's an insider tip: financial institutions typically highlight whatever rate makes their product look most appealing—usually the nominal rate for loans and the EAR/APY for deposits. Being aware of this marketing tactic helps you make more informed decisions.
Practical Application of EAR in US Financial Decisions
How does understanding EAR actually help with your everyday financial choices? Let's explore some real-world applications where this knowledge directly impacts your wallet.
For savings accounts, comparing APYs (which are effectively EARs) is essential for maximizing your returns. As of early 2025, the national average APY for savings accounts is approximately 0.41%, according to FDIC data.
But here's where knowledge becomes power: high-yield savings accounts from various institutions offer APYs ranging from around 4% to over 5%—a massive difference that could multiply your interest earnings tenfold. Since these accounts typically compound daily or monthly, the advertised APY already reflects the effective annual rate.
The same principle applies when shopping for Certificates of Deposit (CDs). The national average APY for a 1-year CD was around 1.89% in mid-March 2025. However, with a bit of research, you can find competitive rates from various banks and credit unions pushing above 4% for different CD terms.
As with savings accounts, CD interest usually compounds daily or monthly, and the stated APY already factors in this compounding effect.
When it comes to borrowing, understanding EAR reveals the actual cost of loans in a way that might surprise you. Take credit cards, for instance. A card with an advertised 18% annual interest rate compounded monthly has an EAR of approximately 19.72% [(1 + 0.18/12)^12 - 1].
That 1.72% difference might seem small until you realize that on a $5,000 balance, it means paying an extra $86 in interest over a year—not insignificant when you're trying to climb out of debt.
When comparing loan offers, calculating the EAR gives you a more accurate basis for decision-making. For example, if you're looking at a $10,000 loan with a 10% nominal rate compounded monthly (EAR ≈ 10.47%), you'd actually pay more interest than with a 10.2% nominal rate compounded annually (EAR = 10.2%).
Focusing on the effective rate rather than just the flashy advertised rate provides a clearer picture of your actual debt burden across different borrowing options.
Interpreting EAR in the US Context
When you've calculated an EAR, what does that number actually tell you? Let's put these percentages into perspective within the American financial landscape.
Different financial products naturally fall into different EAR ranges. Knowing these typical ranges helps you quickly spot whether what you're being offered is competitive, average, or potentially predatory.
Savings accounts generally offer APYs (EARs) ranging from near 0% in traditional brick-and-mortar banks to about 5% at online banks and credit unions focused on competitive rates.
CDs typically range from below 2% to over 4%, depending on the term length and institution. Money market accounts usually fall within a similar range to CDs.
What about when you're borrowing? Credit card interest rates—which directly impact the EAR if you carry a balance—vary widely but commonly fall between 15% and 30%, sometimes even higher for cards marketed to those with lower credit scores.
So how do you use this information when comparing financial offers? When looking at investment opportunities with different compounding schedules, calculate the EAR for each option using the nominal rate and compounding frequency provided.
By comparing these EAR values directly, you can identify which option is financially advantageous over a one-year period (assuming similar risk profiles).
For instance, if you're choosing between two investments—one offering 6% compounded quarterly (EAR ≈ 6.14%) and another offering 6.05% compounded monthly (EAR ≈ 6.23%)—the second option actually provides a better annual return despite the nominal rates suggesting otherwise.
This kind of comparison cuts through marketing language and reveals which option truly puts more money in your pocket over time. It's like having X-ray vision that sees through the financial industry's promotional packaging.
Conclusion: Leveraging EAR for Sound Financial Choices
Understanding Effective Annual Rate cuts through marketing hype to reveal what you're actually earning or paying. It's your financial X-ray vision.
For investments, comparing APYs (not nominal rates) shows which opportunities truly deliver better returns. For loans, calculating the EAR exposes costs that flashy advertised rates conveniently minimize.
While fees, risks, and specific terms also matter, mastering EAR gives you the confidence to see past misleading rates and choose options that align with your financial goals.
In personal finance, seeing the complete picture is half the battle—EAR gives you that clarity.

FAQ
The effective annual rate (EAR) is calculated using the formula: EAR = (1 + r/n)^n – 1, where r is the nominal interest rate and n is the number of compounding periods per year. This formula accounts for the effect of compound interest over multiple periods within a year.
The EFF (Effective Annual Rate) formula is: EFF = (1 + r/n)^n – 1, where r is the nominal interest rate and n is the number of compounding periods per year. This formula converts a nominal interest rate to an effective annual rate, accounting for the impact of compounding.
APR (Annual Percentage Rate) is the simple interest rate for a year without accounting for compounding, while EIR (Effective Interest Rate) factors in the effect of compounding. EIR is typically higher than APR and provides a more accurate representation of the actual cost of borrowing or return on investment.
The effective annual rate of 7% compounded monthly is approximately 7.23%. This is calculated using the formula: EAR = (1 + 0.07/12)^12 – 1. The result shows that monthly compounding increases the actual annual return compared to the stated 7% rate.
Effective Annual Rate Calculator: Compare True Interest Costs Solutions Tailored to Real Life 🧮
- Deliver results you can actually trust
- Effective ways to crunch complex numbers
- Calculator solutions that make sense for humans

The Numbers Don't Lie:
Why People Actually Use Ultimate Calculators
We built these tools because we got tired of calculators that either oversimplify the math or make you feel like you need an engineering degree to get an answer. Whether you're planning a project or just trying to figure out what something will cost, our calculators give you the straight numbers without the runaround.
Real Reviews From Real Humans
"Finally, a calculator that doesn't make me guess what half the fields mean. Got my answer in 30 seconds."
 Mike RodriguezHomeowner - Denver, CO
Mike RodriguezHomeowner - Denver, CO
100% Free Calculations
Our math works, our prices don't
24/7 Calculator Access
Crunch numbers whenever you need
100% Accurate Results
We double-check our math so you don't have to